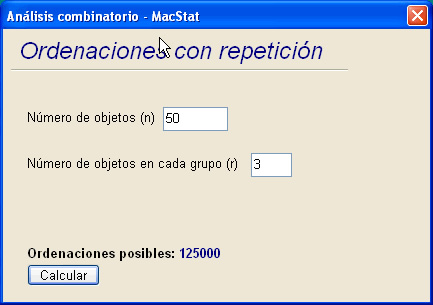
Figura 1. Esta pantalla pertenece a la opción Ordenaciones
con repetición,
en las casillas correspondientes introduzca los datos.
Este módulo contiene un menú con las opciones:
Desde este submenú es posible elegir las opciones para calcular
ordenaciones, ordenaciones con repetición, combinaciones, combinaciones
con repetición, permutaciones, permutación circular, permutación
circular con repetición y coeficiente multinomial.
Este submenú permite obtener probabilidades de las distribuciones:
uniforme, binomial, binomial negativa, geométrica, poisson, hipergeométrica
y normal estándar (con media 0 y desviación estándar1,
o valores de la tabla Z).
Número de objetos
En esta casilla introduzca el número de objetos totales.
Número de objetos en cada grupo
En esta casilla introduzca el número de objetos que hay dentro de cada
grupo, esto es, de cuantos en cuantos objetos se van a tomar. La figura 1 muestra
una pantalla de ejemplo.

Figura 1. Esta pantalla pertenece a la opción Ordenaciones
con repetición,
en las casillas correspondientes introduzca los datos.
Ordenaciones
Se llaman ordenaciones de n objetos de tamaño
r
a los diferentes grupos ordenados que se pueden formar al escoger r
objetos de un grupo de n (donde
r<n),
de tal manera que dos ordenaciones se consideran distintas si difieren
en el orden de sus objetos o en el orden de ellos.
Ordenaciones con repetición
Son ordenaciones en dónde puede repetirse uno o varios objetos,
por lo que es posible que el orden r de una ordenación
con repetición sea mayor que el número n de
objetos dados.
Combinaciones
Una combinación es el número de formas posibles en las
que pueden seleccionarse r objetos de un total de n.
La manera en que se acomoden los objetos no importa.
Combinaciones con repetición
Una combinación es el número de formas posibles en las
que pueden seleccionarse r objetos de un total de n,
donde es posible que un elemento se repita más de una vez.
Permutaciones
Las permutaciones de n objetos son ordenaciones
de
r objetos (donde r = n), las
permutaciones ayudan a resolver problemas en donde es necesario determinar
el número de formas diferentes en que un grupo de tamaño
n
puede ser ordenado.
Permutación circular
Es el número de permutaciones posibles que se dan cuando se permutan
arreglos de objetos que se encuentran acomodados en forma circular (como
personas alrededor de una mesa). Estas permutaciones se consideran diferentes
cuando a un objeto de un arreglo le precede o les sigue (en la misma dirección)
uno diferente al correspondiente en el otro arreglo.
Permutaciones circulares con repetición
Este tipo de permutaciones circulares ocurre cuando los objetos se agrupan
en
r grupos para permutarse.
Coeficiente Multinomial
Es el número de formas en las que pueden asignarse n objetos distintos de k grupos diferentes. Cada uno de estos grupos contienen n1, n2, ..., nk objetos respectivamente.
Los datos que se piden en esta opción, además del número total de objetos son:
Número de grupos: En esta casilla introduzca el número de grupos que hay en el análisis, el número de grupos puede ser de 2 a 100.
Número de objetos por grupo: En cada casilla introduzca
el número de objetos que hay en el grupo correspondiente, recuerde
que la suma de los objetos de todos los grupos debe ser igual a el número
total de objetos.
En estas casillas hay que introducir el intervalo de la variable aleatoria
X del que se desea obtener la probabilidad. MacStat ofrece gran flexibilidad
ya sea para obtener la probabilidad de un valor en específico o
de un intervalo de la variable aleatoria.
Ejemplos:
|
|||||||||||||||||||||||||||||||||||||||
Cada uno de los valores que puede tomar la variable aleatoria X, tiene
una misma probabilidad de ocurrir.
Número de elementos: En esta casilla introduzca el número
de elementos, por ejemplo, si desea obtener la probabilidad de obtener
un resultado de entre 5 posibles, introduzca 5.
Distribución Binomial
Es la distribución del número de éxitos en n
ensayos (observaciones) tomadas de un proceso de Bernoulli. Deben cumplirse
las siguientes condiciones: Los ensayos son independientes entre si, los resultados
posibles pueden ser éxito o fracaso y la probabilidad de
éxito es la misma durante todos los ensayos. Para introducir los
datos se presenta una ventana como se muestra en la figura 2.
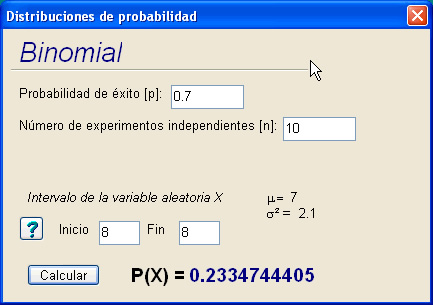
Probabilidad de éxito. En esta casilla ponga el valor
de la probabilidad de éxito p. MacStat obtiene automáticamente
q.
Número de experimentos. En esta casilla ponga el número
de experimentos independientes.
Distribución Binomial negativa
Es la distribución del número de ensayos hasta que ocurre el k-ésimo éxito. Esta distribución también se conoce como la distribución de Pascal.
Esta distribución tiene muchas aplicaciones particularmente en problemas que involucran tiempos de espera y en ciertos tipos de muestreo industrial para detectar cierto número de defectos.
Número de éxitos. En esta casilla ponga el número de éxitos que se desean obtener en el x-ésimo ensayo.
Probabilidad de éxito. En esta casilla ponga la probabilidad
de éxito p.
El intervalo de la variable aleatoria X (Número
de intentos) se usa como se indica al inicio de esta sección.
En estas casilla ponga el número de ensayos X, esto es, el número
de intentos en los que se desea obtener el k-ésimo éxito.
Distribución Geométrica
Es el caso especial de la binomial negativa cuando k = 1, y nos da la probabilidad de que el primer éxito ocurrirá en el n-ésimo ensayo o intento.
Las distribuciones binomial, binomial negativa y geométrica involucran ensayos independientes de Bernoulli con probabilidad constante de éxito para todos los ensayos. Las distribuciones difieren con respecto al procedimiento de muestreo.
El intervalo de la variable aleatoria X se
usa como se indica al inicio de esta sección (distribuciones).
Probabilidad. En esta casilla introduzca el valor de probabilidad
de que un evento ocurra por primera vez en el x-ésimo intento.
Distribución Hipergeométrica
Cuando la población es infinita o el muestreo es con remplazo el modelo apropiado es la distribución binomial.
Para el caso de que la población es finita y el muestreo es sin remplazo, los ensayos sucesivos no son idénticos ni independientes, por lo que la probabilidad de un éxito cambia de ensayo a ensayo. El modelo apropiado es la distribución hipergeométrica.
El intervalo de la variable aleatoria X se usa como se indica al inicio de esta sección (distribuciones).
Número de elementos. En esta casilla introduzca el número de elementos o ensayos totales.
Tamaño de la muestra. En esta casilla ponga el número de elementos de la muestra (n) seleccionada del total N de elementos.
Número de éxitos. En esta casilla ponga el número
de éxitos que se obtienen de la muestra n.
Distribución de Poisson
La distribución de Poisson es una distribución de probabilidad discreta, que guarda una similitud muy cercana a la binomial.
La distribución de Poisson generalmente se emplea para describir el patrón de comportamiento de un proceso en el cuál algún evento de interés sobre un intervalo contínuo de tiempo, longitud o espacio.
El intervalo de la variable aleatoria X se
usa como se indica al inicio de esta sección (distribuciones).
Promedio de observaciones por unidad de tiempo [lambda]. En
esta casilla ponga el promedio de observaciones por unidad de tiempo.
Por ejemplo:
Si el promedio de llegadas a una fila es de 5 observaciones por unidad
de tiempo (puede ser segundo, minuto, hora etc.) hay que poner 5, por otro
lado, si se sabe que el promedio es de 12 cada 5 unidades de tiempo, entonces
el promedio por unidad es (12/5) = 2.4 observaciones por UNIDAD de tiempo,
entonces ponga 2.4
Distribución Normal estándar
La distribución normal teórica es especificada por un modelo matemático. Cualquier distribución normal puede ser transformada a la distribución normal estándar (con media 0 y varianza 1), la cuál considerablemente simplifica el cálculo de áreas bajo la curva normal.
Valor de Z. Esta parte calcula numéricamente el valor de la distribución normal estándar (con media 0 y varianza 1) para un valor Z. El valor que obtenga es el que encontrará en la tabla Z.
Por ejemplo:
Si quiere obtener el valor para Z=2.18 ponga 2.18, MacStat le dará
el área acumulada (desde la parte izquierda hasta el valor dado),
y también el área que falta (el área comprendida entre
el valor dado y la parte derecha de la curva).